Skip to main content

METODE GREEDY, DIVIDE AND CONQUER

METODE GREEDY

     Metode/Algoritma Greedy merupakan algoritma yang membentuk solusi langkah per langkah. Pada setiap langkah tersebut akan dipilih keputusan yang paling optimal. Keputusan tersebut tidak perlu memperhatikan keputusan selanjutnya yang akan diambil, dan keputusan tersebut tidak dapat diubah lagi pada langkah selanjutnya.

a. Prinsip Utama Algoritma Greedy
Prinsip utama algoritma greedy adalah ?take what you can get now!?. Maksud dari prinsip tersebut adalah sebagai berikut: Pada setiap langkah dalam algoritma greedy, kita ambil keputusan yang paling optimal untuk langkah tersebut tanpa memperhatikan konsekuensi pada langkah selanjutnya. Kita namakan solusi tersebut dengan optimum lokal. Kemudian saat pengambilan nilai optimum lokal pada setiap langkah, diharapkan tercapai optimum global, yaitu tercapainya solusi optimum yang melibatkan keseluruhan langkah dari awal sampai akhir.
Contoh kasus algoritma greedy :
Misalkan tersedia koin : 1, 3, 5.
Uang senilai X=8 dapat di tukar dengan cara :
§  1+1+1+1+1+1+1+1 = 8 (8 koin)
§  1+1+1+1+1+3=8 (6 koin)
§  1+1+1+5=8 (4 koin)
§  1+1+3+3=8 (4 koin)
§  3+5=8 (2 koin)                                    solusi optimal.
Maka solusi optimal dari kasus penukaran koin di atas adalah 2 koin.
 METODE GREEDY banyak digunakan dalam berbagai penyelesaian maslah, antara lain adalah :
1.    Optimal Storage on Tapes Problem
2.    Kanpsack Problem
3.    Minimum Spanning Tree Problem
4.    Shortest Path Problem

Knapsack Problem
Knapsack problem adalah suatu masalah bagaimana cara menentukan pemilihan barang dari sekumpulan barang di mana setiap barang tersebut mempunyai berat dan profit masing masing, sehingga dari pemilihan barang tersebut didapatkan profit yang maksimum.
Contoh kasus knapsack
§  w1 = 10;  p1 = 2
§  w2 = 5;     p2 = 3
§  w3 = 15;   p3 = 5
§  w4 = 7;     p4 = 7
§  w5 = 6;     p5 = 1
§  w6 = 18;   p6 = 4
§  w7 = 3;     p7 = 1
M = 15
Jawaban :    

Properti objek
Greedy by
Solusi
Optimal
i
wi
pi
pi/wi
profit
weight
density
1
2
10
5
1
1
1
1
2
3
5
1,7
1
1
0
1
3
5
15
3
1
0
1
1
4
7
7
1
0
0
0
0
5
1
6
6
1
1
1
1
6
4
18
4,5
1
1
1
1
7
1
3
3
0
1
1
0
Total bobot :
15
11
13
15
Total keuntungan :
54
42
52
54

Kesimpulan : Pada soal ini, algoritma greedy dengan strategi pemilihan objek berdasarkan profit memberikan solusi optimal, sedangkan pemilihan objek berdasarkanweight dan density tidak memberikan solusi optimal.

b. Elemen Algoritma Greedy
        Elemen-elemen yang digunakan dalam penerapan algoritma greedy antara lain :

1. Himpunan Kandidat
        Himpunan yang berisi elemen pembentuk solusi.
2. Himpunan Solusi
        Himpunan yang terpilih sebagai solusi persoalan.
3. Fungsi Seleksi
        Fungsi yang memilih kandidat yang paling mungkin untuk mencapai solusi optimal.
4. Fungsi Kelayakan
       Fungsi yang memeriksa apakah suatu kandidat yang dipilih dapat memberikan solusi yang layak.    Maksudnya yaitu apakah kandidat tersebut bersama dengan himpunan solusi yang sudah terbentuk      tidak melanggar kendala yang ada.
5. Fungsi Solusi
       Fungsi yang mengembalikan nilai boolean. True jika himpunan solusi yang sudah tebentuk               merupakan solusi yang lengkap; False jika himpunan solusi belum lengkap.
6. Fungsi Objektif
        Fungsi yang mengoptimalkan solusi.

c. Skema Umum Algoritma Greedy
        Misal kita mengasumsikan elemen algoritma greedy sebagai berikut :
    Himpunan Kandidat = C,
    Himpunan Solusi = S,
    Fungsi Seleksi = select(),
    Fungsi Kelayakan = feasible(),
    Fungsi Solusi = solution(), dan
    Fungsi Obyektif = objective().

        Skema umum dari algoritma greedy dapat kita tuliskan :
- Inisialisasi S dengan kosong.
- Pilih sebuah kandidat dari C (dengan select()).
- Kurangi C dengan kandidat yang telah terpilih di atas.
- Periksa apakah kandidat yang dipilih tersebut bersama ? sama dengan S membentuk solusi yang         layak (dengan feasible()). Jika ya, masukkan kandidat ke S; jika tidak buang kandidat tersebut dan      tidak perlu ditelaah lagi.
- Periksa apakah S yang sudah terbentuk telah memberikan solusi yang lengkap (dengan solution()).      Jika ya, berhenti; jika tidak, ulangi dari langkah 2.

Sumber :  
http://stephanusar.blogspot.com/2012/11/pengertian-metode-greedy-dan-algoritma.html
https://kevinkarundeng.wordpress.com/2012/11/05/contoh-soal-algoritma-greedy-dan-knapsack-problem/
   

   DIVIDE AND CONQUER

   Algoritma Divide and Conquer adalah strategi pemecahan masalah yang besar dengan cara melakukan pembagian masalah yang besar tersebut menjadi beberapa bagian yang lebih kecil secara rekursif hingga masalah tersebut dapat dipecahkan secara langsung. Solusi yang didapat dari setiap bagian kemudian digabungkan untuk membentuk sebuah solusi yang utuh.
   
   Skema umum Algoritma Divide and Conquer


   Contoh kasus dan pemyelesaian
>> Persoalan Minimum dan Maksimum (MinMaks)
Persoalan : Misalnya diketahui table A yang berukuran n eleman sudah berisi nilai integer. Kita ingin menentukan nilai minimum dan nilai maksimum sekaligus di dalam table tersebut. Misalkan tabel A berisi elemen-elemen sebagai berikut :

Ide dasar algoritma secara Divide and Conquer :

Ukuran table hasil pembagian dapat dibuat cukup kecil sehingga mencari minimum dan maksimum dapat diselesaikan (SOLVE) secara lebih mudah. Dalam hal ini, ukuran kecil yang dipilih adalah 1 elemen atau 2 elemen.
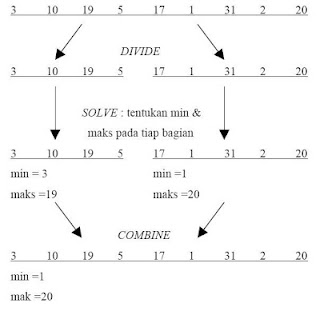
Algoritma MinMaks :
1. Untuk kasus n = 1 atau n = 2,
SOLVE : Jika n = 1, maka min = maks = An. Jika n = 2, maka bandingkan kedua elemen untuk menentukan min dan maks.

2. Untuk kasus n > 2,
DIVIDE : Bagi dua table A secara rekursif menjadi dua bagian yang berukuran sama, yaitu bagian kiri dan bagian kanan.
CONQUER : Terapkan algoritma Divide and Conquer untuk masing-masing bagian, dalam hal ini min dan maks dari table bagian kiri dinyatakan dalam peubah min1 dan maks1, dan min dan maks dari table bagian kanan dinyatakan dalam peubah min2 dan maks2.
COMBINE : Bandingkan min1 dan min2 untuk menentukan min table A, serta bandingkan maks1 dan maks2 untuk menentukan maks table A.


=======================================================
Penyelesaian dengan Algoritma Divide and Conquer secara umum :
=======================================================
a. Asumsi : n = 2k dan titik-titik diurut berdasarkan absis (x).
b. Algoritma Closest Pair :
- SOLVE : jika n = 2, maka jarak kedua titik dihitung langsung dengan rumus Euclidean.
- DIVIDE : Bagi titik-titik itu ke dalam dua bagian, PLeft dan PRight, setiap bagian mempunyai                            jumlah titik yang sama
- CONQUER :Secara rekursif, terapkan algoritma D-and-C pada masingmasing bagian.
- Pasangan titik yang jaraknya terdekat ada tiga kemungkinan letaknya :
  Pasangan titik terdekat terdapat di bagian PLeft.
  Pasangan titik terdekat terdapat di bagian PRight.
 Pasangan titik terdekat dipisahkan oleh garis batas L, yaitu satu titik di PLeft dan satu titik di PRight.
   Jika kasusnya adalah (c), maka lakukan tahap COMBINE untuk mendapatkan jarak dua titik terdekat sebagai solusi persoalan semula.



Sumber : 
http://wawanhermawan74.blogspot.com/2012/10/contoh-kasus-algoritma-divide-and.html

Comments

Post a Comment

Popular posts from this blog

PERBEDAAN ANTARA ILMU SOSIAL DASAR DAN ILMU BUDAYA DASAR

Ilmu Sosial Dasar adalah ilmu yang mengkaji mengenai masalah-masalah sosial yang terjadi didalam masyarakat. Ilmu sosial dasar ini sangat penting untuk diterapkan didalam masyarakat karena dengan mempelajari ilmu sosial dasar ini masyarakat dapat mengatasi masalah sosial yang sering terjadi sehingga tidak menimbulkan perpecahan antar masyarakat. Ilmu sosial dasar ini saat ini sudah masuk ke dalam kurikulum pembelajaran di perguruan tinggi dengan tujuan untuk menanamkan nilai-nilai sosial sehingga para mahasiswa dapat memahami bahwa adanya kenyataan-kenyataan sosial dan masalah-masalah yang selalu ada didalam masyarakat, menyadari bahwa setiap masalah sosial bahwa setiap masalah sosial yang timbul dalam masyarakat itu bersifat kompleks dan cara penyelesaiannya hanya dengan mempelajarinya, peka dan tanggap/cekatan terhadap masalah-masalah sosial yang ada didalam masyarakat untuk ikut serta dalam upaya menanggulangi masalah-masalah sosial tersebut. Ruang lingkup ilmu sosial dasar men...
Post a Comment
Read more

Arti dari Sebuah Keindahan

Keindahan Apa sih keindahan itu? Dalam Kamus Besar Bahasa Indonesia, keindahan diartikan sebagai keadaan yang enak dipandang, cantik, bagus benar atau elok. Keindahan dipelajari sebagai bagian dari estetika, sosiologi, psikologi sosial, dan budaya. Sebuah "kecantikan yang ideal" adalah sebuah entitas yang dikagumi, atau memiliki fitur yang dikaitkan dengan keindahan dalam suatu budaya tertentu, untuk kesempurnaannya. Keindahan adalah sifat-sifat yang merujuk kepada sesuatu yang indah di mana manusia mengekspresikan perasaan indah tersebut melalui berbagai hal yang mengandung unsur estetis yang dinilai secara umum oleh masyarakat. Menurut The Liang Gie dalam bukunya “ Garis Besar Estetik” (Filsafat Keindahan), dalam bahasa Inggris Keindahan diterjemahkan dengan kata “Beautiful”, bahasa Perancis “Beau” , Italia dan Spanyol “Bello” , kata-kata itu ber asal dar i bahasa Latin “Bellum” , akar katanya adalah “Bonum” yang berarti Kebaikan kemudian mempunyai bentuk pengecila...
Post a Comment
Read more